คณิตศาสตร์

อัตรส่วน

อัตราส่วน  อย่างหนึ่งที่แสดงถึงจำนวนหรือขนาดตามสัดส่วนเมื่อเปรียบเทียบกับอีกปริมาณหนึ่งที่เกี่ยวข้องกัน อัตราส่วนจะเป็นปริมาณที่ไม่มีหน่วย หากอัตราส่วนนั้นเกี่ยวข้องกับปริมาณที่อยู่ในมิติ เดียวกัน และเมื่อปริมาณสองอย่างที่เปรียบเทียบกันเป็นคนละชนิดกัน หน่วยของอัตราส่วนจะเป็นหน่วยแรก "ต่อ" หน่วยที่สอง ตัวอย่าง เช่น ความเร็วสามารถแสดงได้ในหน่วย "กิโลเมตรต่อชั่วโมง" เป็นต้น ถ้าหน่วยที่สองเป็นหน่วยวัดเวลา เราจะเรียกอัตราส่วนชนิดนี้ว่า อัตรา (rate)

ทั้งเศษส่วนและอัตราร้อยละเป็นอัตราส่วนที่นำเอาไปใช้เฉพาะทาง เศษส่วนเป็นปริมาณส่วนหนึ่งที่เทียบกับปริมาณทั้งหมด ในขณะที่อัตราร้อยละจะแบ่งปริมาณทั้งหมดออกเป็น 100 ส่วน นอกจากนั้น อัตราส่วนอาจสามารถเปรียบเทียบปริมาณได้มากกว่าสองอย่างซึ่งพบได้น้อยกว่า เช่นสูตรอาหาร หรือการผสมสารเคมี เป็นต้น

อัตราส่วน 2:3 (สองต่อสาม) หมายความว่าปริมาณทั้งหมดประกอบขึ้นจากวัตถุแรก 2 ส่วนและวัตถุหลังอีก 3 ส่วน ดังนั้นปริมาณวัตถุจะมีทั้งหมด 5 ส่วน หรืออธิบายให้เจาะจงกว่านี้ ถ้าในตะกร้ามีแอปเปิล 2 ผลและส้ม 3 ผล เรากล่าวว่าอัตราส่วนระหว่างแอปเปิลกับส้มคือ 2:3 ถ้าหากเพิ่มแอปเปิลอีก 2 ผลและส้มอีก 3 ผลลงในตะกร้าใบเดิม ทำให้ในตะกร้ามีแอปเปิล 4 ผลกับส้ม 6 ผล เป็นอัตราส่วน 4:6 ซึ่งก็ยังเทียบเท่ากันกับ 2:3 (แสดงให้เห็นว่าอัตราส่วนก็สามารถลดทอนได้เหมือนกับเศษส่วน) ซึ่งในกรณีนี้ 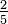 หรือ 40% ของผลไม้ทั้งหมดคือแอปเปิล และ  หรือ 60% ของผลไม้ทั้งหมดคือส้ม หรือกล่าวอีกนัยหนึ่งคือ อัตราส่วน 2:3 ไม่ได้มีความหมายเหมือนกับเศษส่วน 

ร้อยละ (Percent )

ร้อยละ   คือ การเปรียบเทียบจำนวนสองจำนวน โดยให้จำนวนที่สองใน

อัตราส่วนเป็น 100 ใช้สัญลักษณ์    % เช่น  แดงสอบวิชาคณิตศาสตร์ได้คะแนนร้อยละ 85    หมายความว่า   ในคะแ . นนเต็ม 100 คะแนน แดงสอบได้ 85 คะแนน

อัตราส่วนและร้อยละ 1. การเปลี่ยนรูปอัตราส่วนเป็นร้อยละ เมื่อต้องการเปลี่ยนอัตราส่วนในรูปร้อยละ มีวิธีการเปลี่ยนให้อัตราส่วนนั้น อยู่ในรูปของอัตราส่วนใหม่ ที่มีจำนวนหลังเป็น 100 แล้วจำนวนแรกจะเป็นค่า ของร้อยละตามต้องการ ซึ่งมีวิธีคิดอยู่หลายวิธี เช่น จงเขียน     17 : 25    ให้อยู่ในรูปร้อยละ

วิธีที่ 1 = = = = = = = วิธีที่ 2 วิธีที่ 3 =

2. การเปลี่ยนรูปร้อยละเป็นอัตราส่วน เมื่อต้องการเปลี่ยนร้อยละให้อยู่ในรูปอัตราส่วนทำได้โดยเขียนร้อยละนั้นให้เป็นอัตราส่วน ที่มีจำนวนหลังเป็นร้อย   เช่น 25 % = = 1 : 4 = = = = 80 % 4 : 5

การคำนวณค่าเกี่ยวกับร้อยละ การคำนวณค่าเกี่ยวกับร้อยละสามารถคำนวณได้    2    วิธีคือ วิธีที่ 1   :   เขียนสัดส่วนแล้วแก้สมการ วิธีที่ 2   :   เขียนสมการแล้วแก้สมการ ข้อตกลง  : ให้นักเรียนใช้เครื่องหมาย ดังนี้               - ของ ให้ใช้สัญลักษณ์เป็น  x ( คูณ )               - เป็น , อยู่ , คือ , เท่ากับ  ให้เปลี่ยน สัญลักษณ์  เป็น   =

ตัวอย่าง 8%   ของ 75   เท่ากับเท่าไร วิธีที่ 1 ให้   a    แทน   8%   ของ 75 เขียนสัดส่วน ดังนั้น 8%   ของ 75    คือ   6

วิธีที่ 2 ให้   8%   ของ 75   เท่ากับ    a เขียนสมการ ดังนั้น   8%   ของ 75    เท่ากับ   6

การแก้โจทย์ปัญหาเกี่ยวกับร้อยละ นักเรียนสามารถนำความรู้เกี่ยวกับ การคำนวณค่าเกี่ยวกับร้อยละมาช่วยแก้ปัญหาโจทย์เกี่ยวกับร้อยละ ซึ่งจะสรุปหลักการคำนวณทั่วไปดังนี้ 1.   สมมุติตัวแปรในสิ่งที่ต้องการ 2.   สร้างสมการ หรือ สร้างสัดส่วน 3.   แก้สมการหรือแก้สัดส่วนหาค่าตัวแปร  

ความหมายของร้อยละที่ควรทราบ 1.  อัตราดอกเบี้ย 12%  หมายความว่า     เงินต้น 100 บาท ในเวลา 1 ปี ได้ดอกเบี้ย 12 บาท 2.  ขายของได้กำไร 20%  หมายความว่า     ทุน 100 บาท ได้กำไร 20 บาท ขายไปราคา 120 บาท 3.  ขายของขาดทุน 15%  หมายความว่า     ทุน 100 บาท ขาดทุน 15 บาท ขายไปราคา 85 บาท 4.  ลดราคาสินค้า 5%  หมายความว่า     ติดราคาไว้ 100 บาท ลดให้ 5 บาท ขายไปราคา 95 บาท

ตัวอย่างที่ 1 กมลสอบได้สังคมได้ 95% ถ้าคะแนนเต็ม 180 คะแนนจงหาว่ากมลสอบได้กี่คะแนน วิธีทำ สมมติให้    กมลสอบได้          X     คะแนน จะได้      สัดส่วน X x 100   = 180 x 95 X     = X     = 171 ดังนั้น    กมลสอบได้ 171 คะแนน          Ans.

ตัวอย่างที่ 2 ทีมฟุตบอลของโรงเรียนแห่งหนึ่งแข่งขันชนะ 75% ของจำนวนครั้งที่ลงแข่งขัน ถ้าทีมนี้ลงแข่งขัน 24 ครั้ง จะชนะกี่ครั้ง วิธีทำ สมมติให้ ทีมที่ชนะ         Y     ครั้ง จะได้      สัดส่วน Y x 100   = 75 x 24 Y     = X     = 18 ดังนั้น    ทีมฟุตบอลนี้ชนะการแข่งขัน    18   ครั้ง        Ans.